Computational Geometry at USI

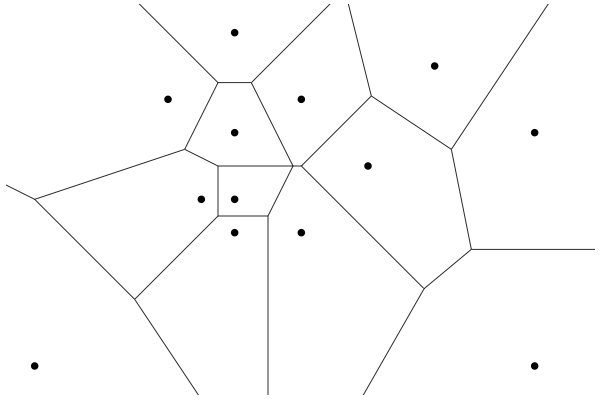
Voronoi diagrams of polygonal objects

We investigate problems on generalized Voronoi diagrams of polygonal objects in Euclidean space \(\mathbb{R}^d\). Voronoi diagrams are among the most fundamental structures in Computational Geometry and they have proved powerful tools in solving diverse computational problems. The standard Voronoi diagram of a set of sites is a subdivision of the plane into regions such that the Voronoi region of a site p is the locus of points closest to p than to any other site. Sites can be points, polygonal objects, or other types of geometric objects. Higher order Voronoi diagrams encode k-nearest neighbor information and they define a partitioning of space into maximal regions such that every point within a region has the same k nearest sites.

Our project is funded by SNF (under project number 127137).

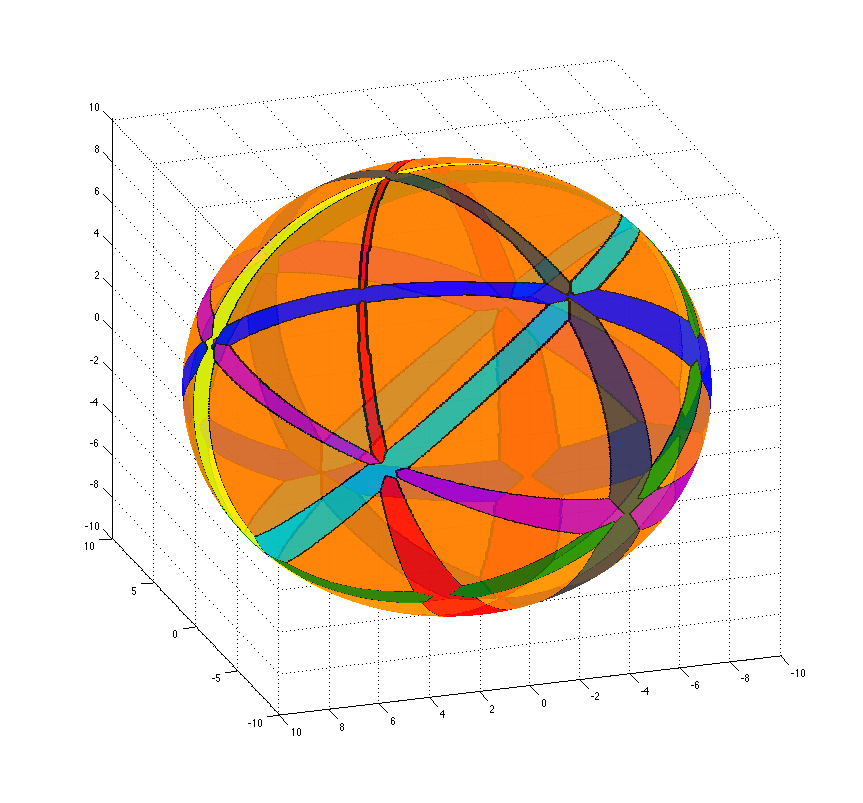
Gaussian map

The Gaussian map encodes information about the unbounded cells of a Voronoi diagram. This structure is of particular interest when all cells are unbounded. For example, all the d-dimensional cells of the farthest Voronoi diagram of segments or lines are unbounded. Roughly speeking, the Gaussian map is the intersection of the diagram with a big circle / hypersphere.

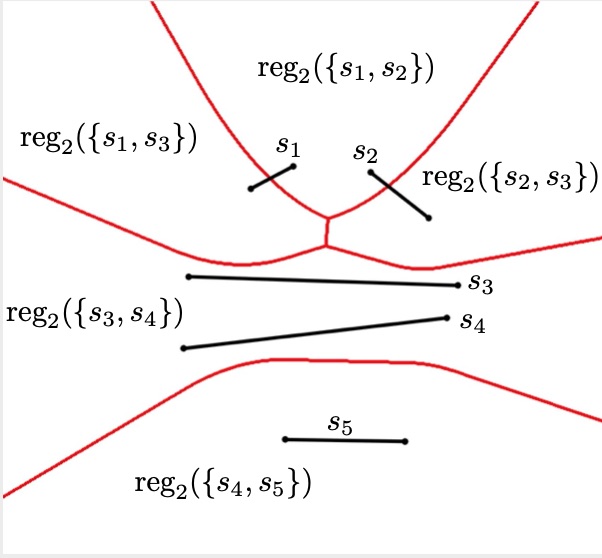
An order-2 Voronoi diagram of 5 segments in 2D

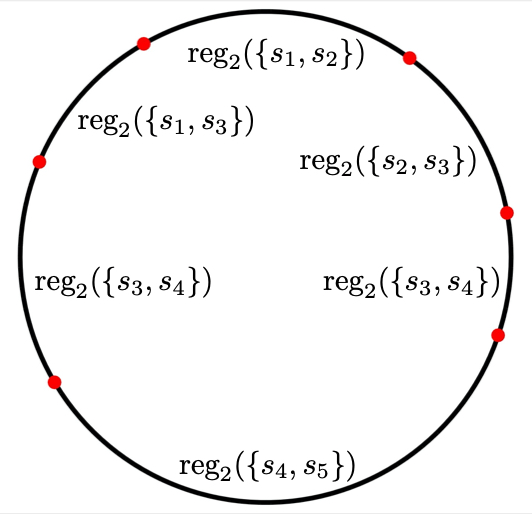
and its Gaussian map.

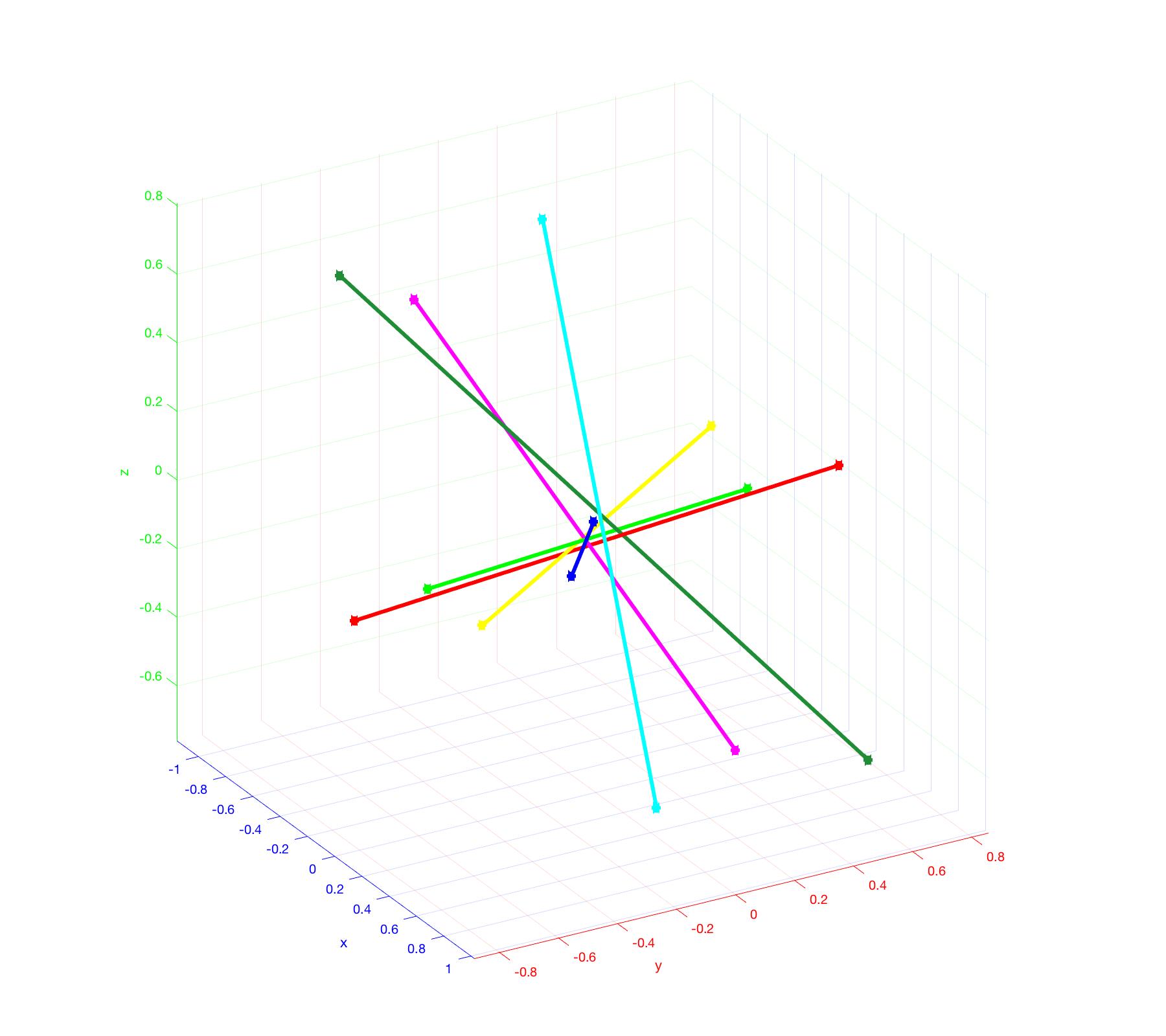
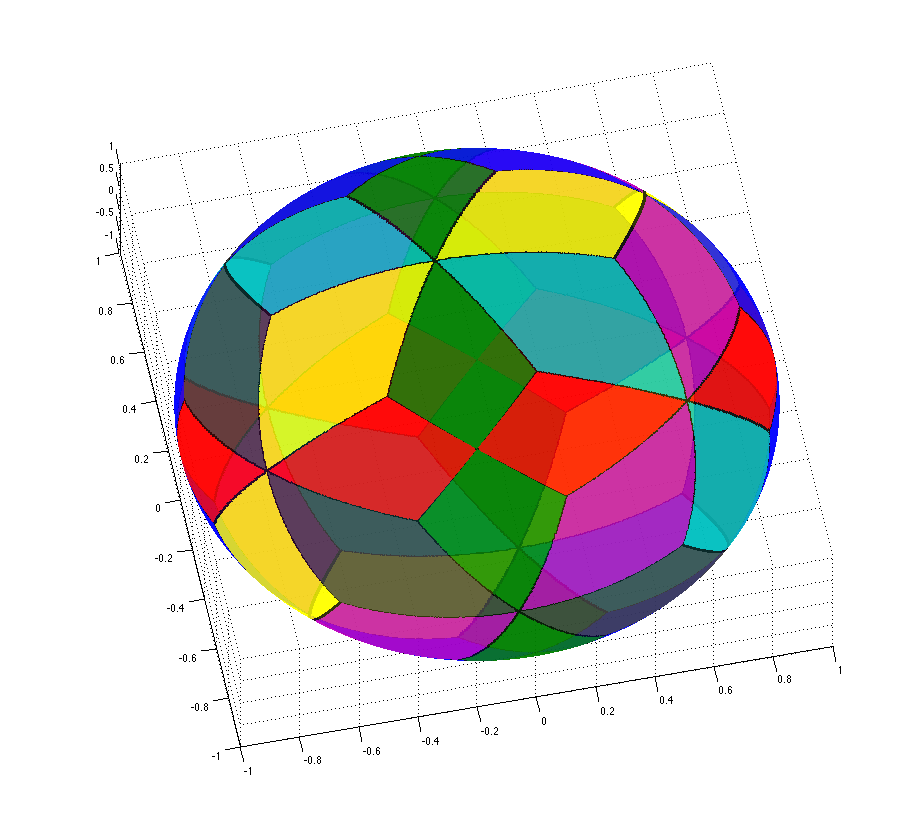
Segments in 3D

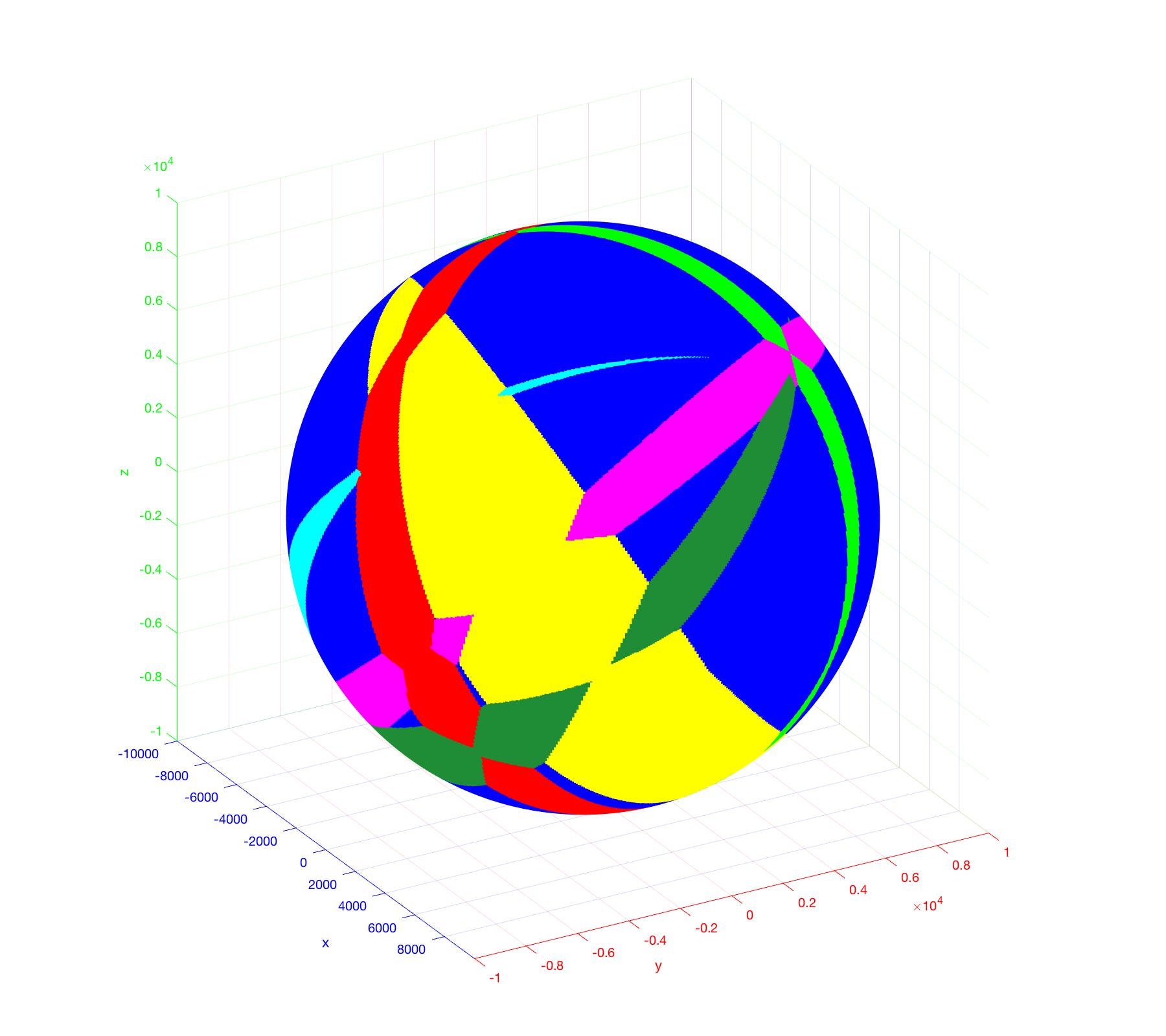
and the Gaussian map of their farthest Voronoi diagram.

The Gaussian map of the order-k Voronoi diagram of n lines or line segments in \(\mathbb{R}^d\) has \(O(\min\{k, n-k\} n^{d-1})\) complexity, which for \(k=n-1\) is tight in worst-case. It can be computed in \(O(n^{d-1} \alpha(n))\) time.

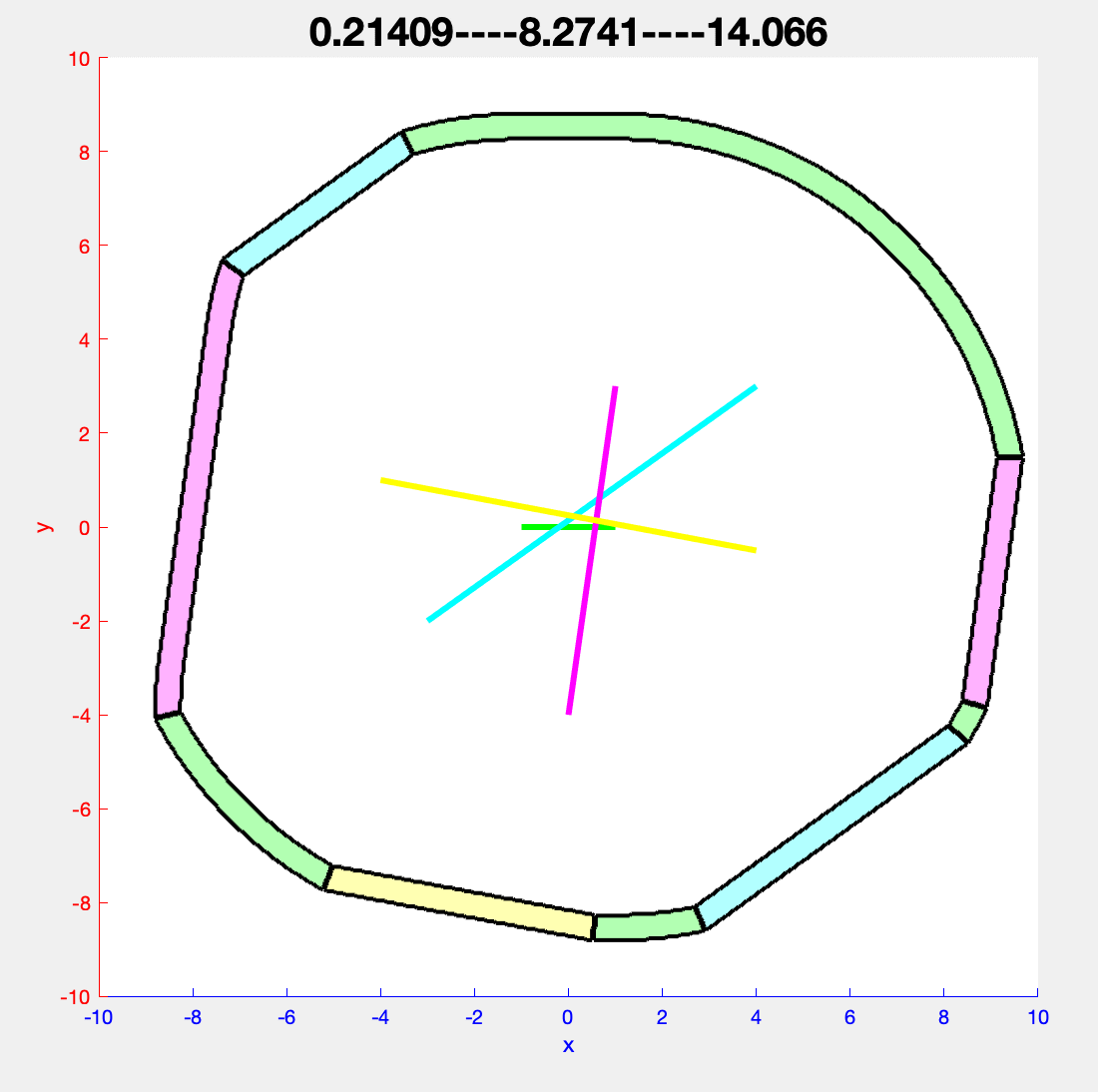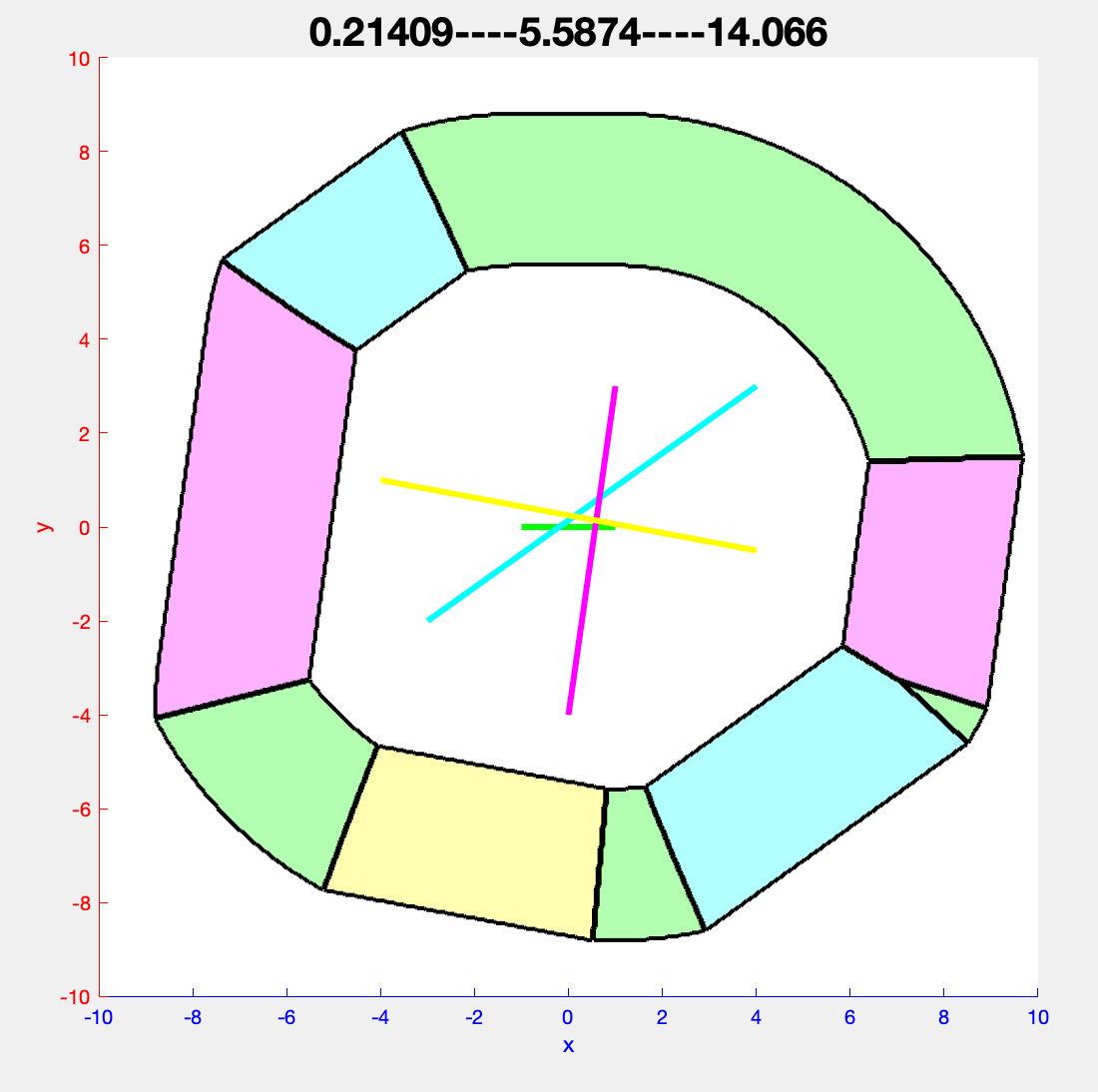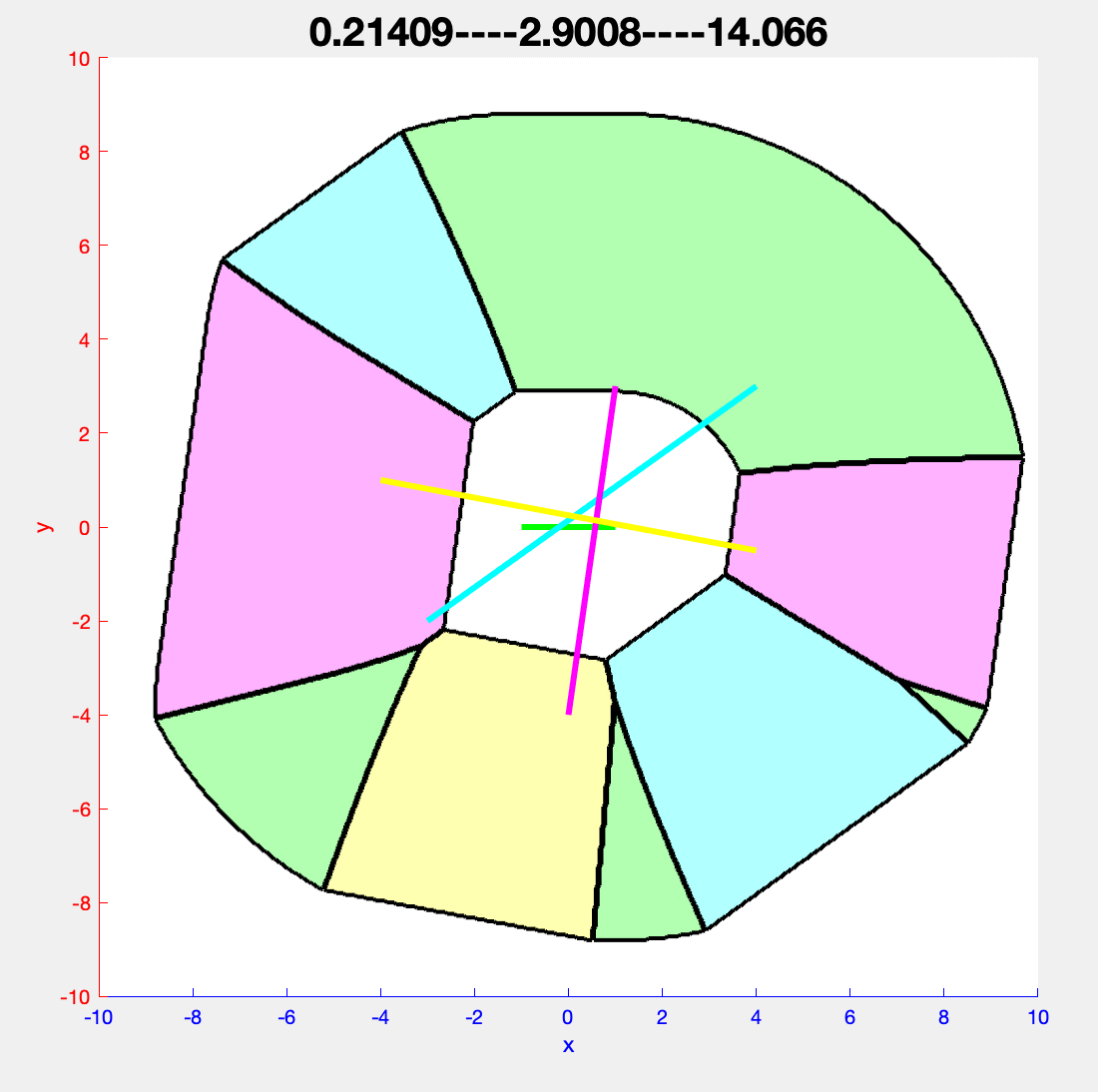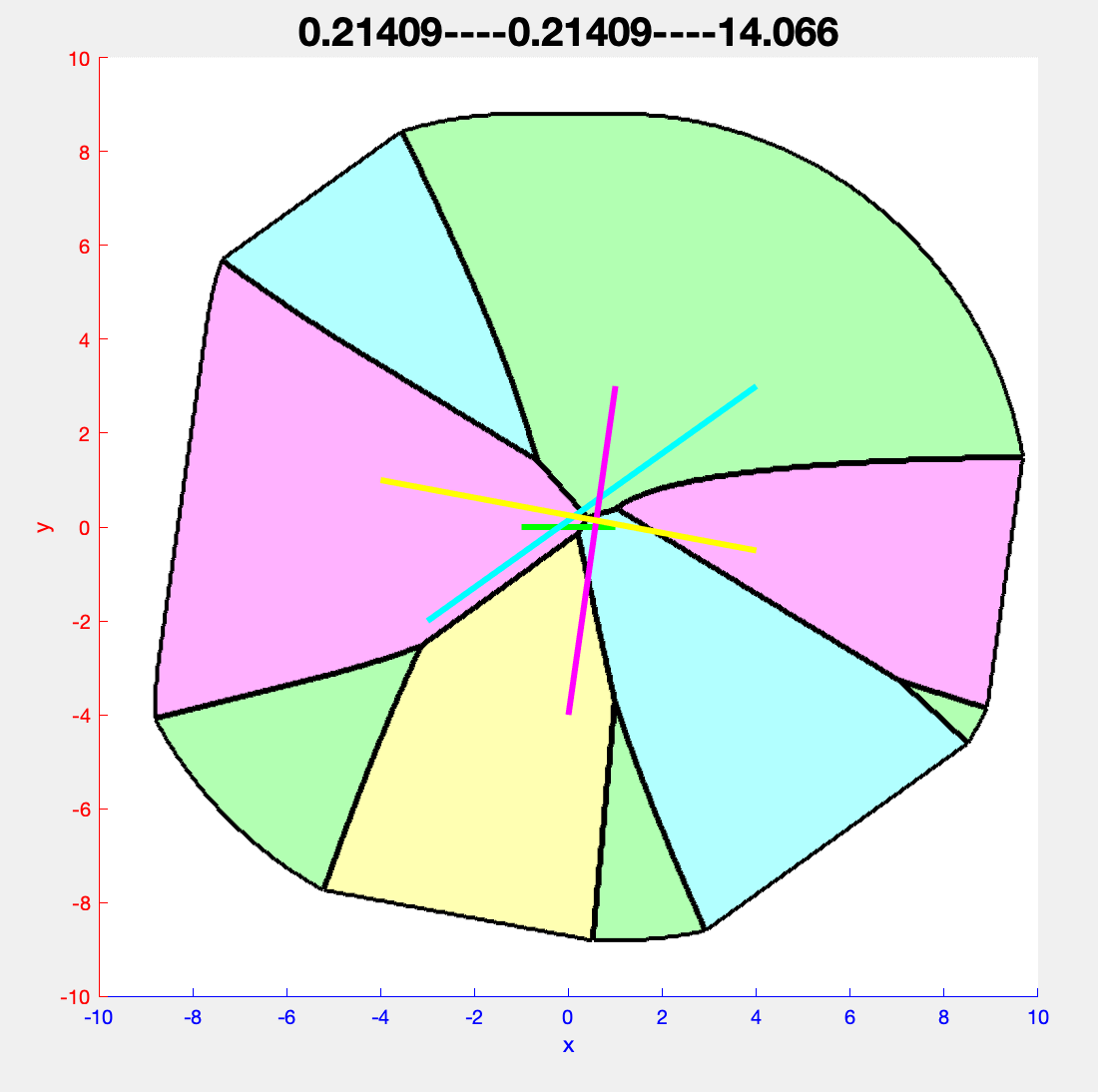
In 2D, the Gaussian map of the farthest Voronoi diagram of line segments can be used to construct the complete diagram. This "collapse algorithm" by Aurenhammer et al. starts from the unbounded edges of the diagram and detects vertices and bounded edges in decreasing distance to their farthest site. This algorithm needs \(O(n \log(n))\) time.

Visualization of the collapse algorithm for 4 segments in 2D. The farthest region of each segment is colored in the same color as the segment itself.

At first sight it might seem that the collapse algorithm, can be generalized to construct the complete three dimensional diagram. However, there are two properties of the diagram in 3D, which make a generalization without additional \(\Theta(n^3)\) time difficult.

1. The trisector of three segments in 3D can be a closed curve.
2. The distance function on the trisector of three lines in 3D can induce a local maximum.

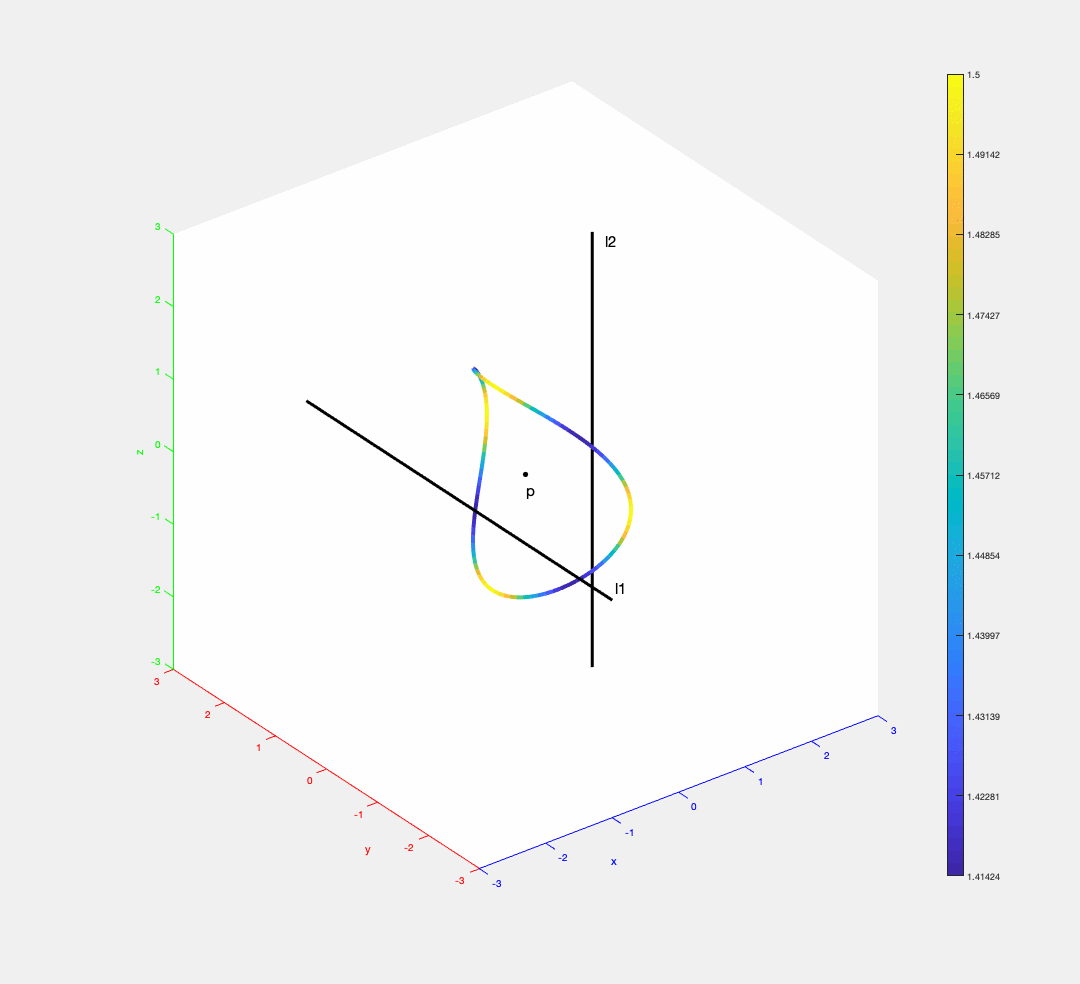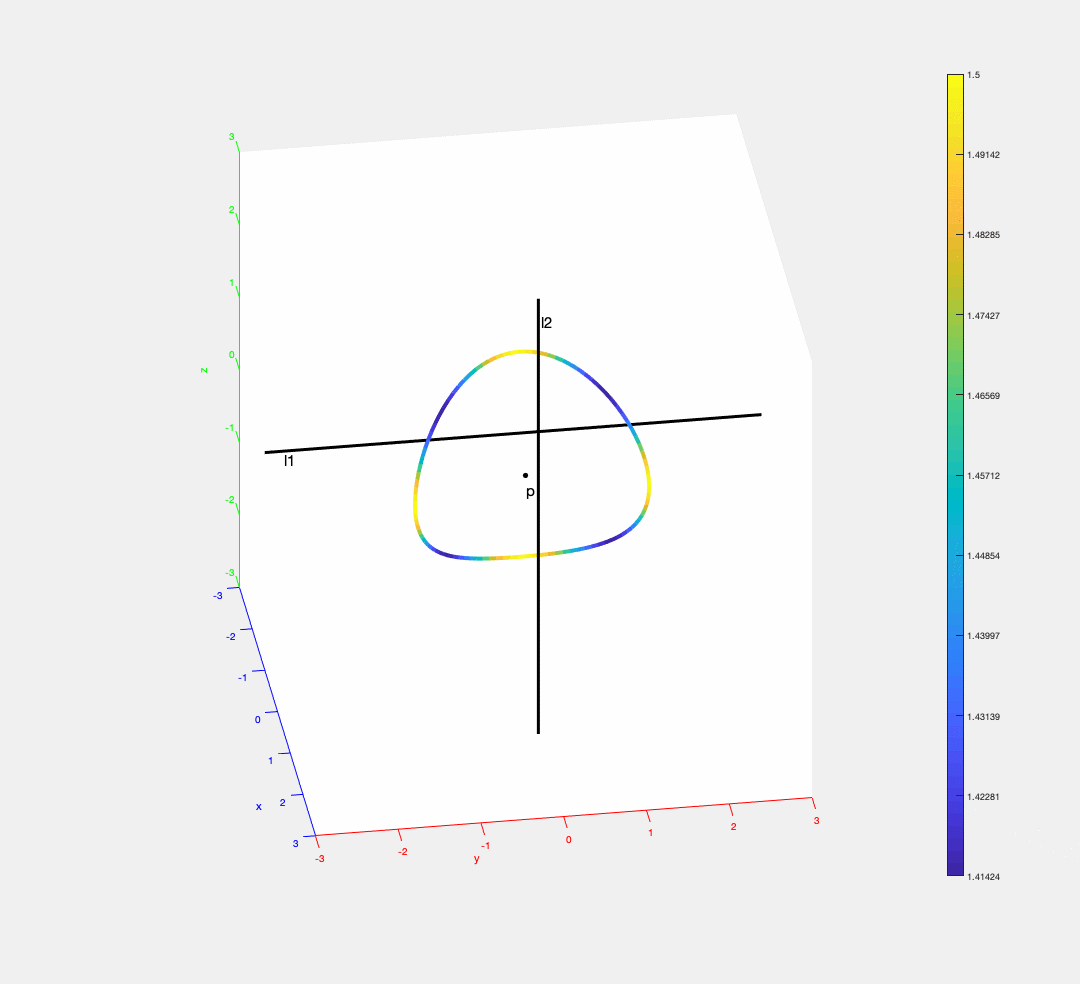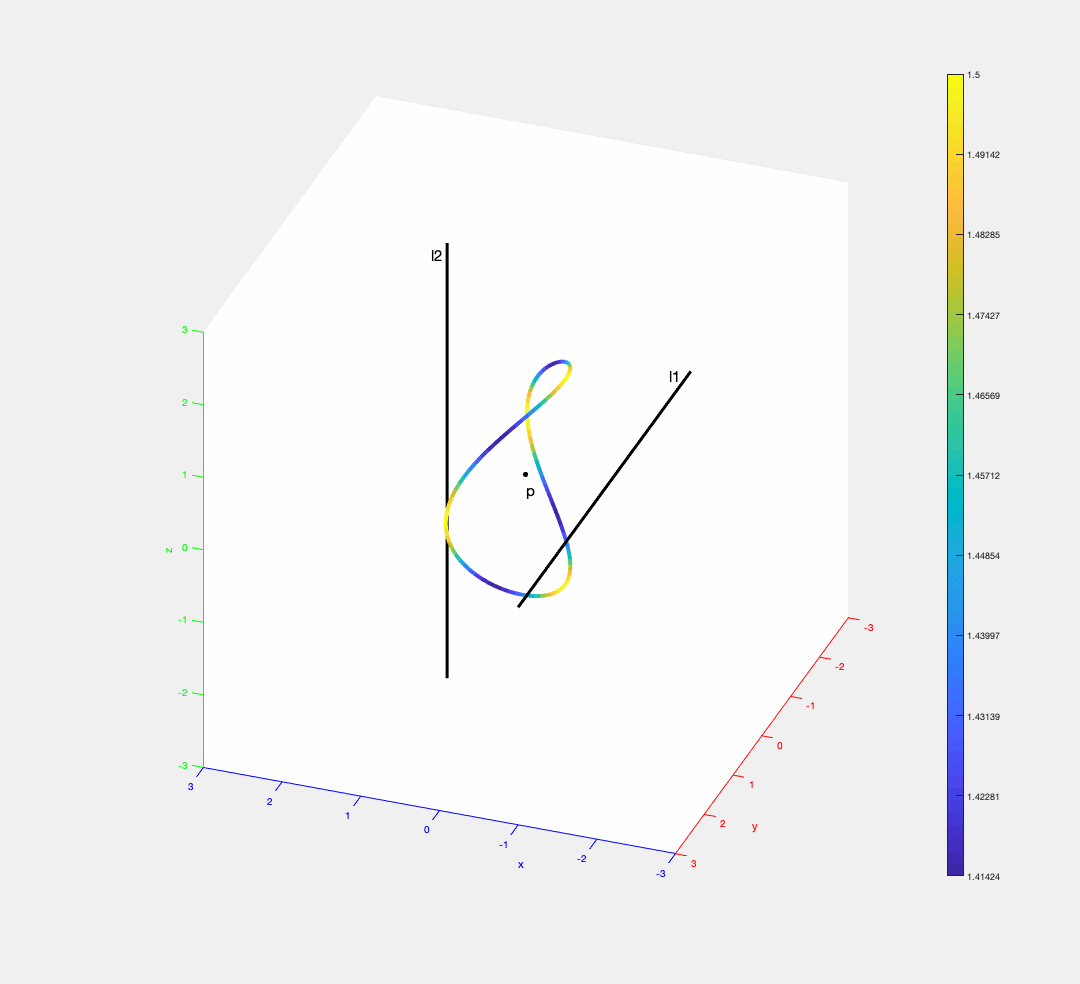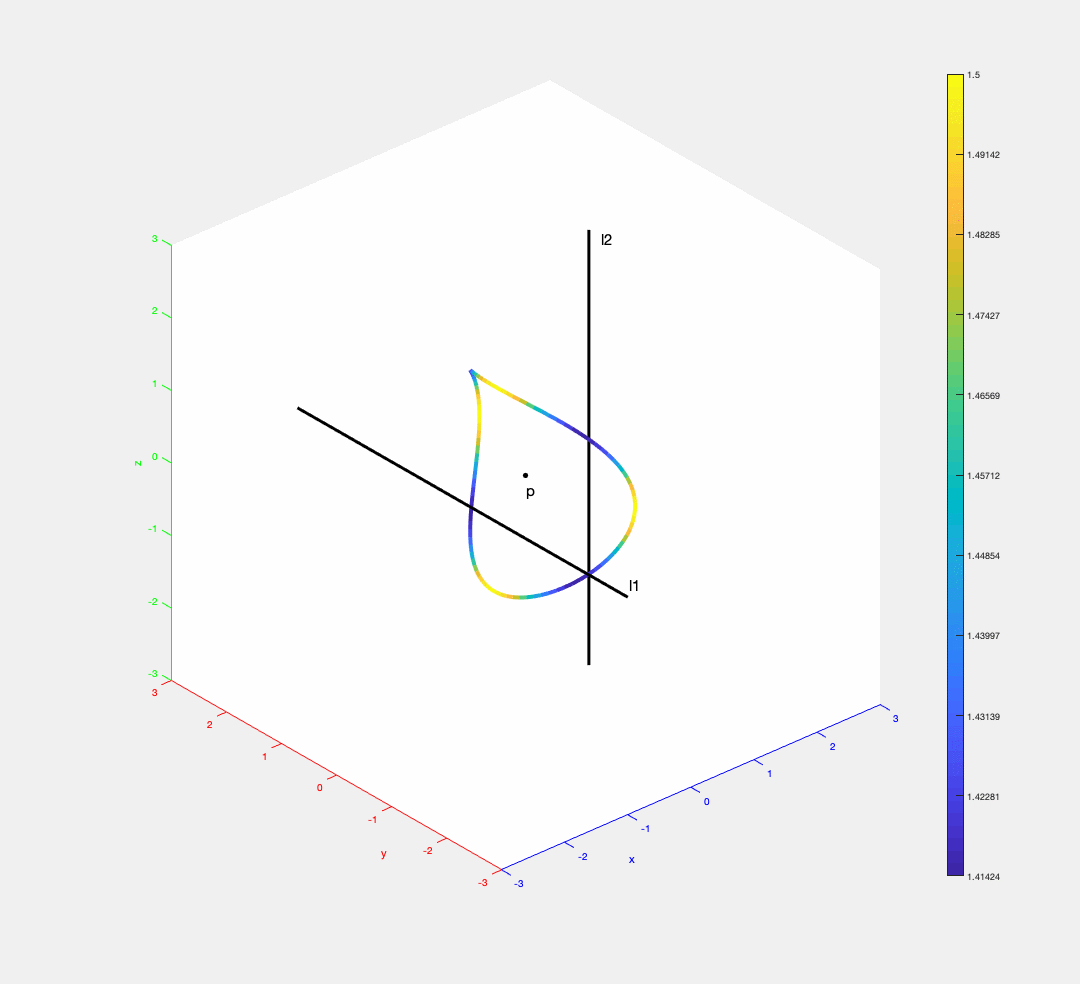
The trisector of three segments (one segment has 0 length) in 3D can be a closed curve. The distance of a point on the trisector to the segments is encoded by colors (blue = small distance, yellow = big distance).

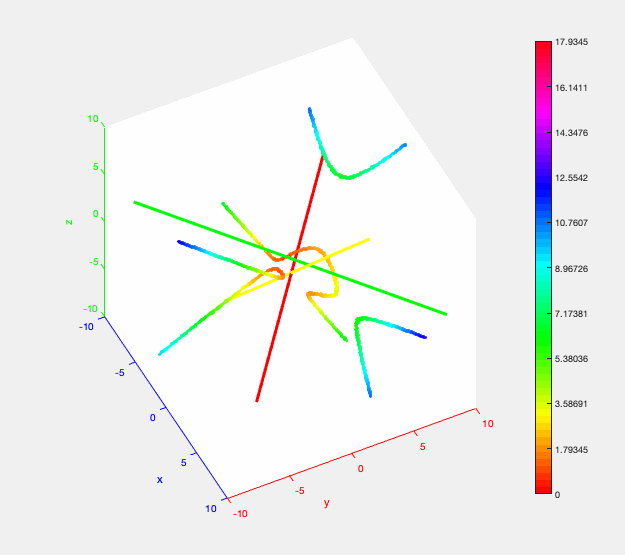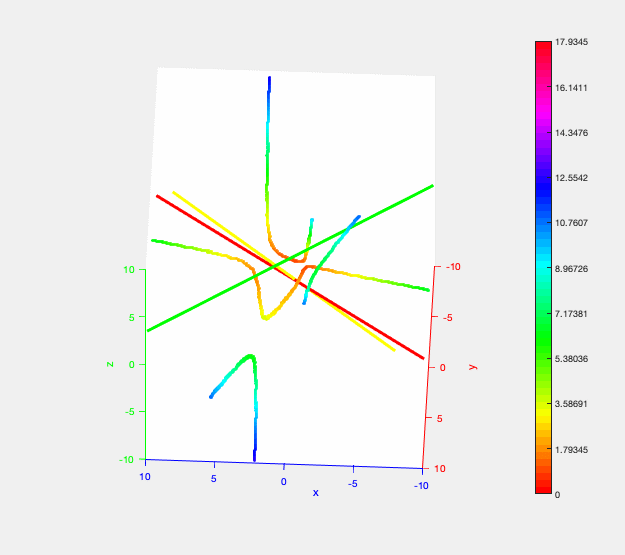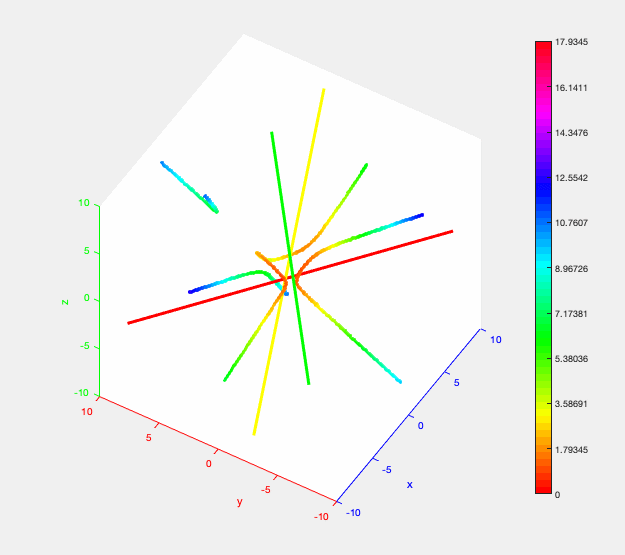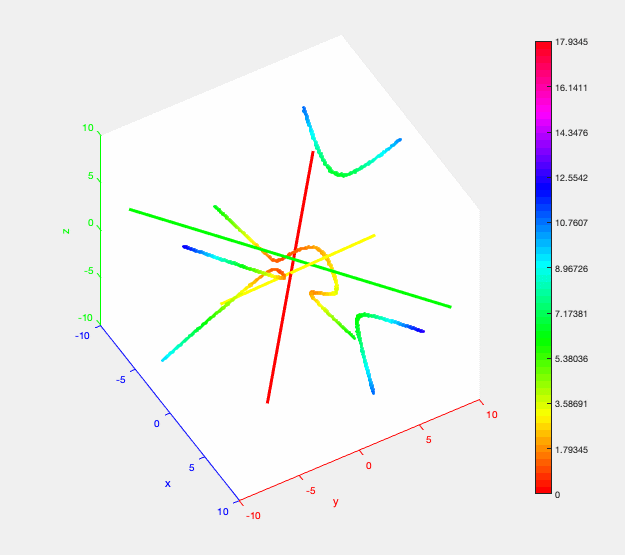
The trisector of 3 lines in 3D. The distance from a point on the trisector to the lines is encoded by colors (small distance = red -> orange -> yellow -> green -> blue = big distance). The distance function restricted to the middle branch of the trisector induces a local maximum (walking along the branch the colors change from ... -> orange -> yellow -> orange -> ...).

Hausdorff and higher order Voronoi diagrams

Spacial Decompositions and Graphs (short nickname: VORONOI) is a collaborative research project. It involves 8 partners from 6 different countries, and it is part of the EuroGIGA program of the European Science Foundation (ESF).

Our group, in particular, investigates problems related to Hausdorff and higher-order Voronoi diagrams in the plane. The objective is to derive a deeper understanding of these fundamental geometric structures, link them with the existing theoretical framework, and produce efficient but simple algorithms for their construction. Diverse application areas can directly benefit from such algorithms. An example is the area of VLSI yield analysis and design manufacturability (DFM), where generalized Voronoi diagrams of polygonal objects have already provided the basis of most advanced design automation tools in the semiconductor industry.

Our individual subproject is funded jointly by SNF (under project number 134355) and ESF.

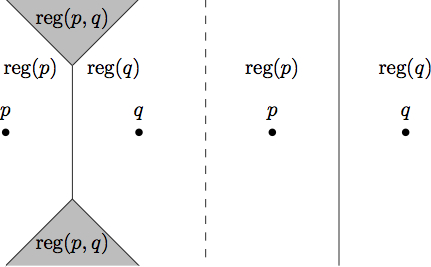
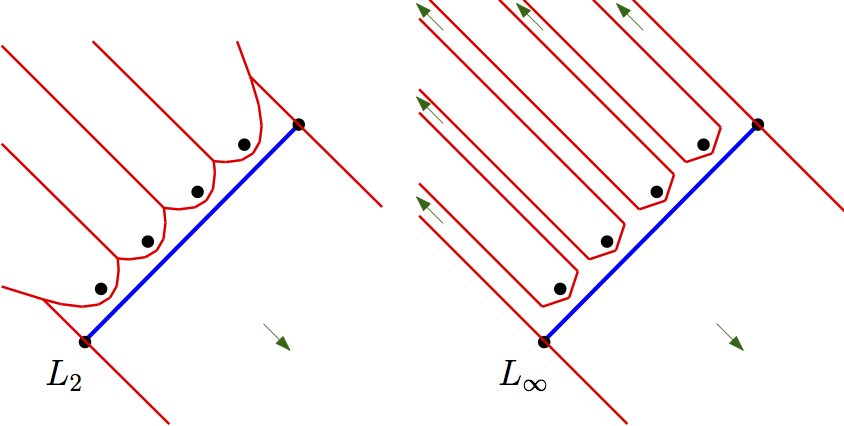
Cluster Voronoi diagrams

Voronoi diagram of a set of sites is a subdivision of a space into maximal regions according to the closeness relation with respect to sites. Voronoi diagram of a set of points in the plain looks like this:
This diagram is widely used in different areas, since it allows answering the proximity queries efficiently. However, approximating the real objects as points is often not precise enough. Then the generalized Voronoi diagrams come into play. Our research is focused on the cases when the sites are sets of points instead of single points (Hausdorff Voronoi diagram of point-clusters, Farthest Color Voronoi diagram, farthest Voronoi diagram of line segments). For example, here is the set of clusters and its Hausdorff Voronoi diagram and Farthest Color Voronoi diagram respectively:
For those structures we are seeking for efficient construction algorithms. Applying the known techniques becomes challenging since those Voronoi diagrams have properties, substantially different from the standard case.
Another fascinating and mainly unexplored direction of research is moving from 2D to 3D. We study the farthest Voronoi diagram of line-segments and lines in 3D. The figures below depict a cross-section of these two diagrams by a sphere of a big radius. We call such cross-section a Gaussian Map, and use it to analyze the behavior of the diagram close to infinity.

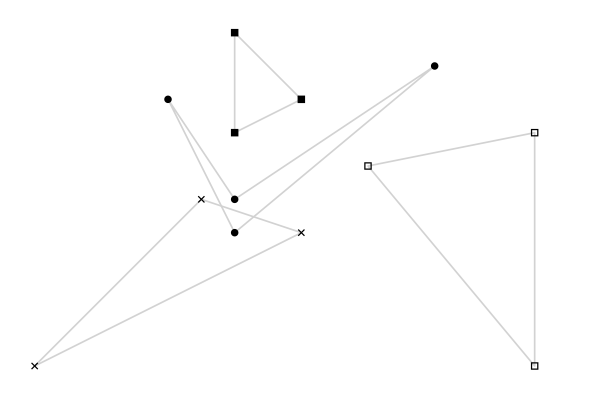
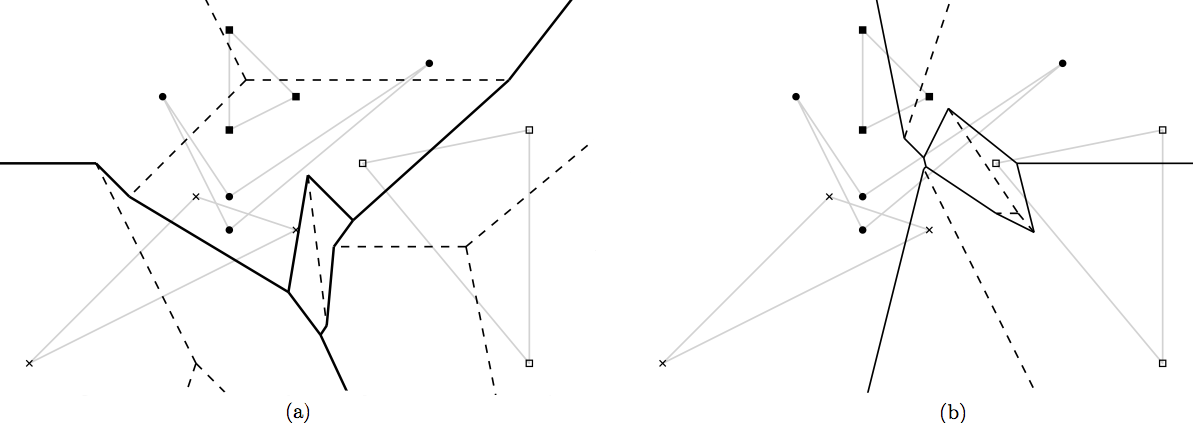
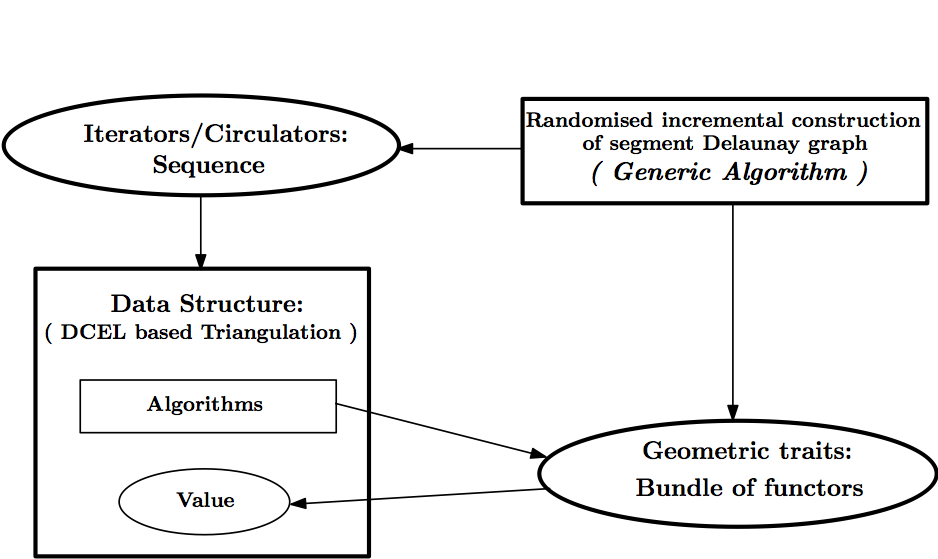
CGAL implementation

Computational Geometry Algorithm Library (CGAL) is a proven industrial standard tool to solve geometric problems in various application domain such as image processing, geometric modelling, EDA etc. The geometric algorithms and data structures in CGAL are implemented under the design goals of robustness, genericity, flexibility, efficiency, and ease of use. These design goals are fulfilled in CGAL by choosing C++ generic programming, using template classes, and function templates.

Our interest is to implement different variants of Voronoi diagram for line segments in the max-norm. The existing segment Voronoi diagram in CGAL is for Euclidean metric and is constructed by a randomised incremental algorithm. There are two template parameters passed to the algorithm in this package, First is the geometric traits class that provides the basic geometric objects (points, segments, parabolic bisectors), the geometric predicates for computing the diagram such as in-circle tests, conflict tests etc. and some basic constructions for visualization of the diagram, and the Second is the triangulation data structure in CGAL for storing the diagram. We exploited the generic implementation of the segment Voronoi diagram in CGAL to write the trait classes for the implementation of the Voronoi diagram in the max-norm that is in a simple piece-wise linear metric. Some interesting challenges were to handle in-square tests, 2-dimensional bisectors, and the max-norm parabolae. The package is integrated with CGAL-4.7. Details can be found here.



We are also interested in other implementation projects in the CGAL environment:
1. Plane sweep algorithm for construction of Voronoi diagrams.
2. Implementing higher order Voronoi diagrams.

VLSI pattern analysis

With the increase in miniaturization of current VLSI patterns, there is a significant rise in printability problems of such patterns, during the photolithography process. The analysis of patterns to find faults or error-prone locations, is of prime importance to the manufacturing process.
We have introduced a fast method to automatically extract patterns based on their structure and context, using the Voronoi diagram of VLSI design shapes. We first identified possible problematic locations, represented as gauge centers, and then use the derived locations to extract windows and problematic patterns from the design layout. The problematic locations are prioritized by the shape and proximity information of design polygons.

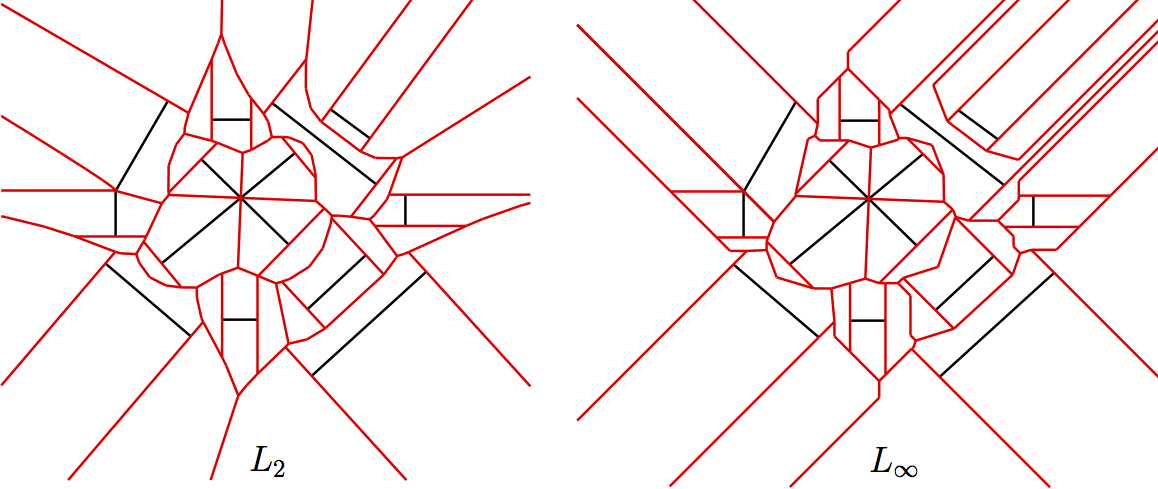
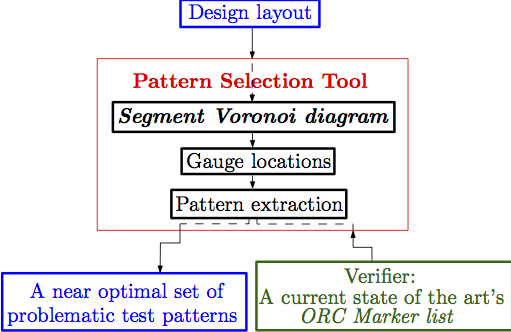
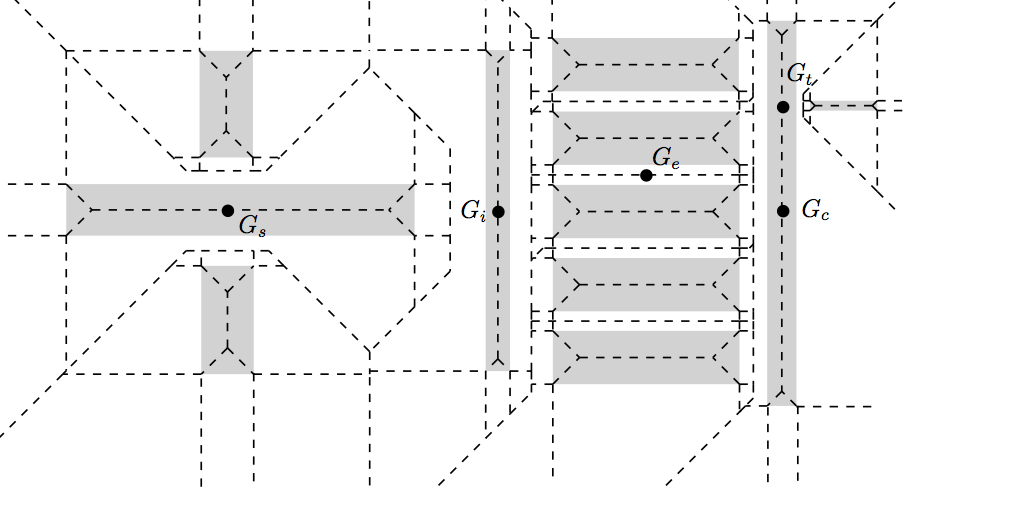
Our work on VLSI pattern analysis has won the Luigi Franco Cerrina Memorial Best Student Paper Award at SPIE Advanced Lithography, Design-Process-Technology Co-optimization for Manufacturability IX, 2015. (pdf)

An interesting future work would be to derive an optimal set of Patterns for model-based OPC (Optical Proximity Correction).

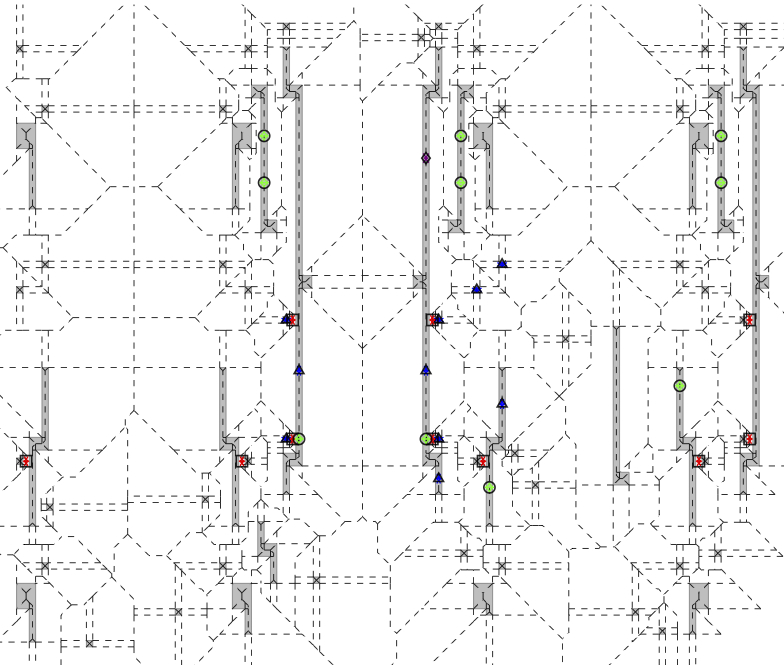
Box Subdivision algorithms

A classic problem in Facility Location is to place a facility in order to serve a given set of demand points or customers such that it minimizes the total transportation costs. The total cost at any point is interpreted as the sum of the distances to the demand points. The point that minimizes this sum is called the Fermat Point. This is an old geometric problem that has inspired scientists over the last three centuries.

A foci set is a non-empty finite set of (demand) points \(X = \{a_1,...,a_k\}\). The Fermat distance function is given by \(\phi(x) = \sum_{a \in X} ||x-a||\). The global minimum \(r^* = \min_{x \in \mathbb{R}^d} \phi(x)\) is called the Fermat radius; any point x that achieves this minimum, is called a Fermat point.

We also consider the closely related problem of computing \(k\)-ellipses of \(X\). For any \(r>r^*(X)\), the level set of the Fermat distance function is \(\phi^{-1}(r) = \{x \in \mathbb{R}^d: \phi(x)=r\}\). If \(k=1\), this level set is a sphere; if \(k=2\), the level set is the classic ellipse if \(d=2\). When \(X\) has \(k\) points, we call \(\phi^{-1}(r)\) a \(k\)-ellipsoid, or \(k\)-ellipse in the planar case. We want to approximate such \(k\)-ellipses, viewed as curves that bound the set of facility locations whose total transportation cost is at most some specified \(r\). More generally, we might want to simultaneously approximate several such \(k\)-ellipes.

See our EuroCG 2020 paper for more details and references. Click here for watching a video that summerizes the most important parts of this paper.

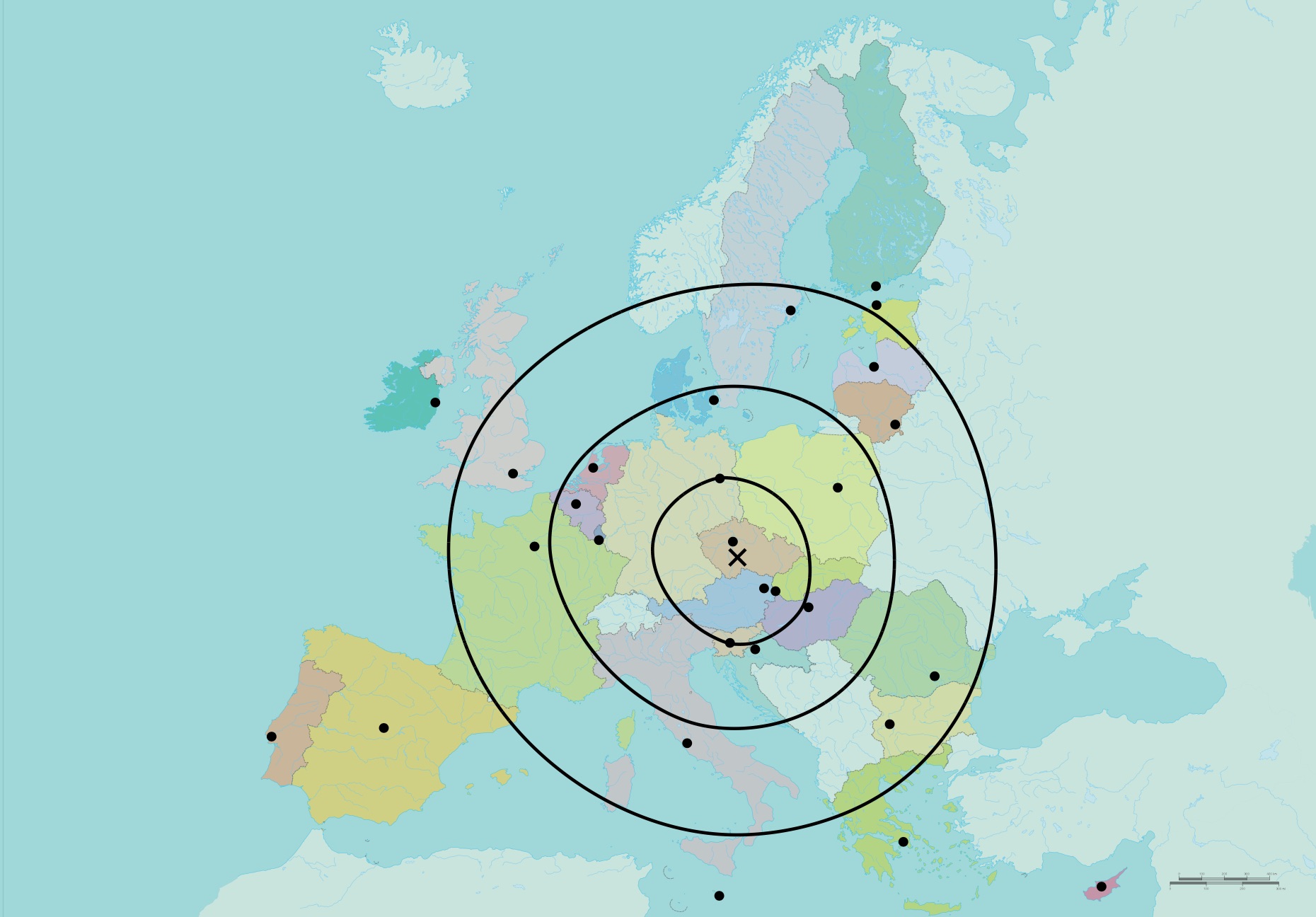The Fermat point of the capitals of Europe marked with \(\times\). Moreover, three 28-ellipses are plotted. The original map was taken from https://www.consilium.europa.eu.

We are computing those approximations by box subdivision type algorithms. The algorithms take an inital box, which contains the area of interest, and keep splitting boxes until:

1. the boxes for sure do not contain an important part of the output (red boxes) or
2. the boxes are small enough.

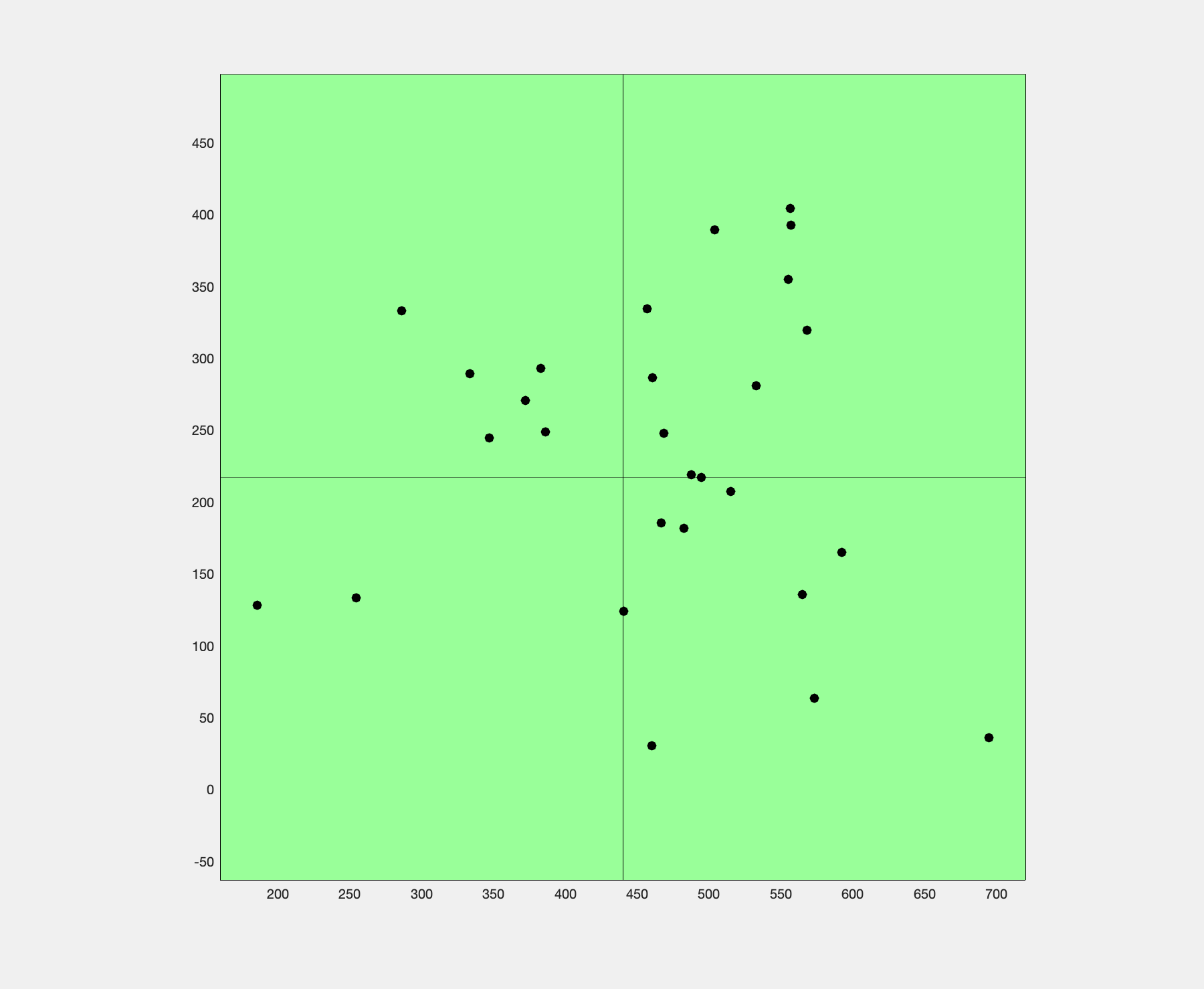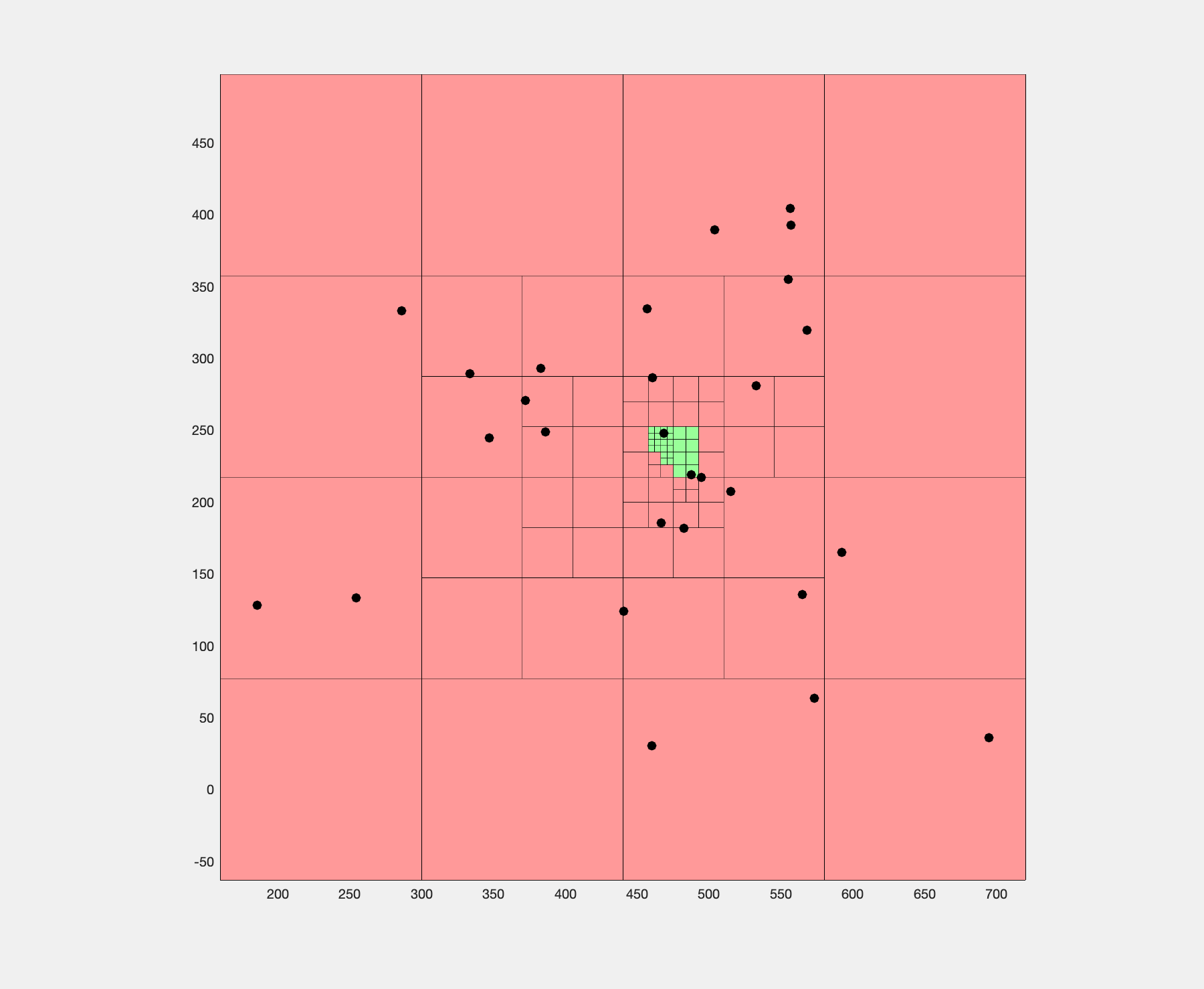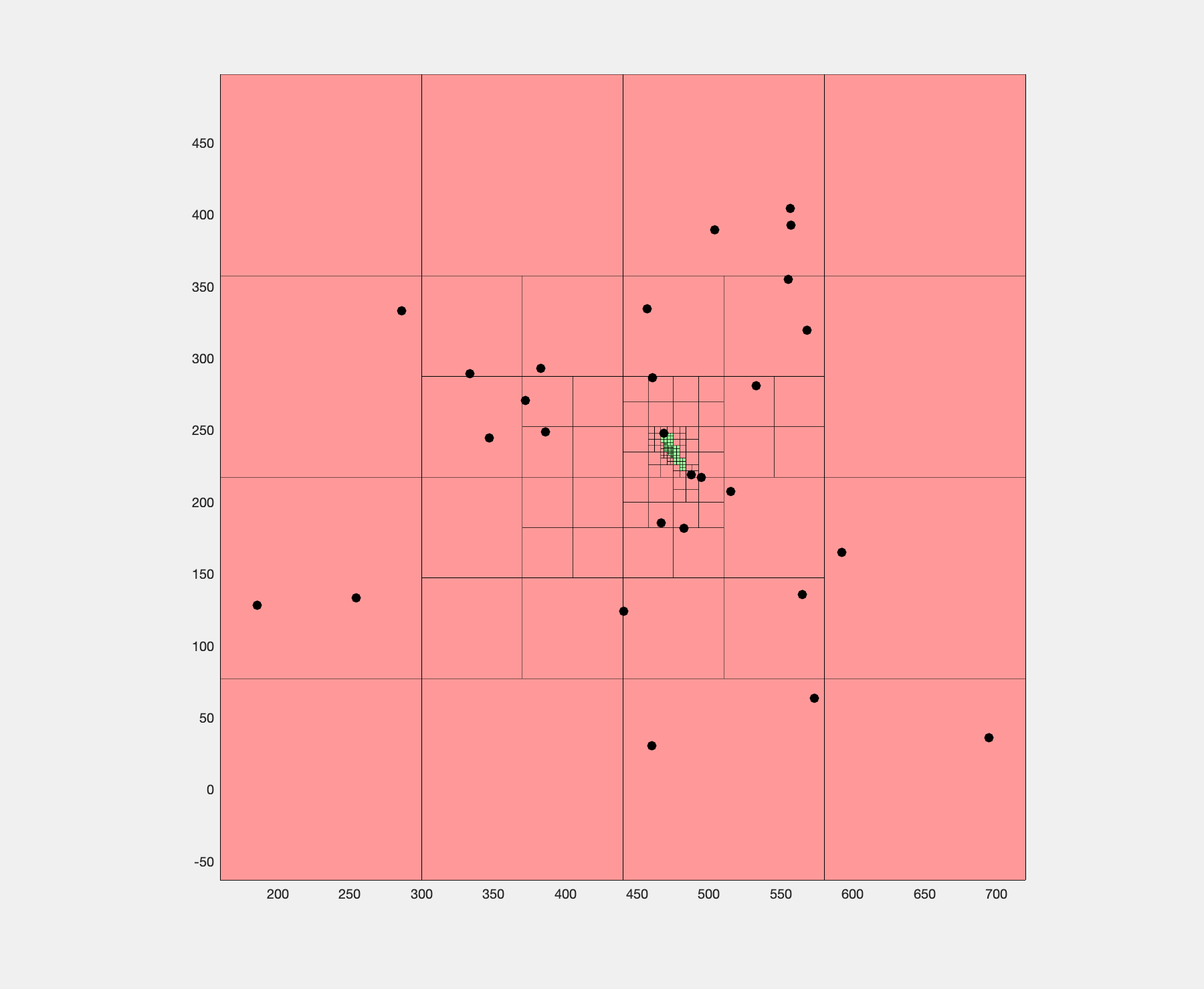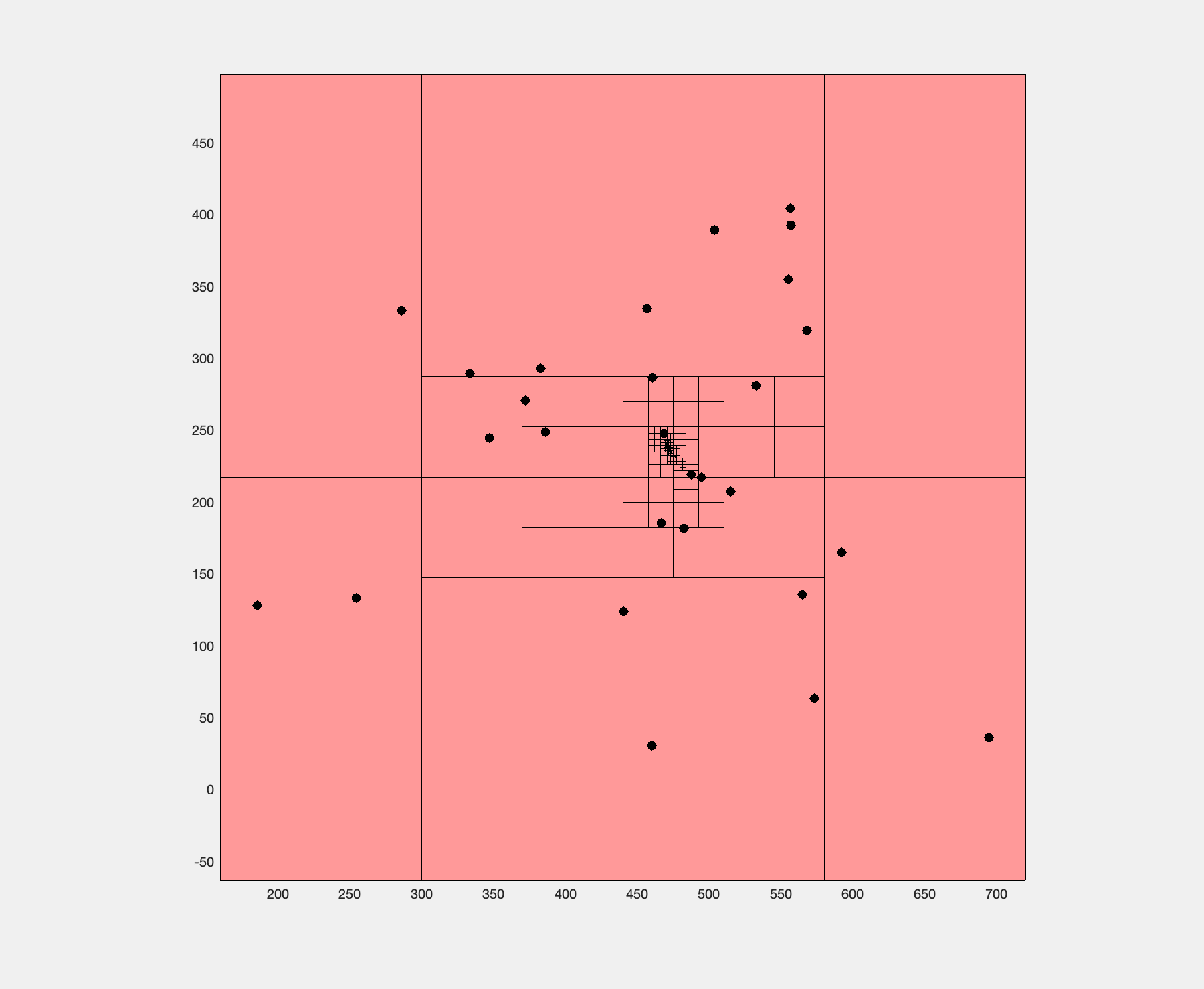
Box subdivision algorithm finding the Fermat point.

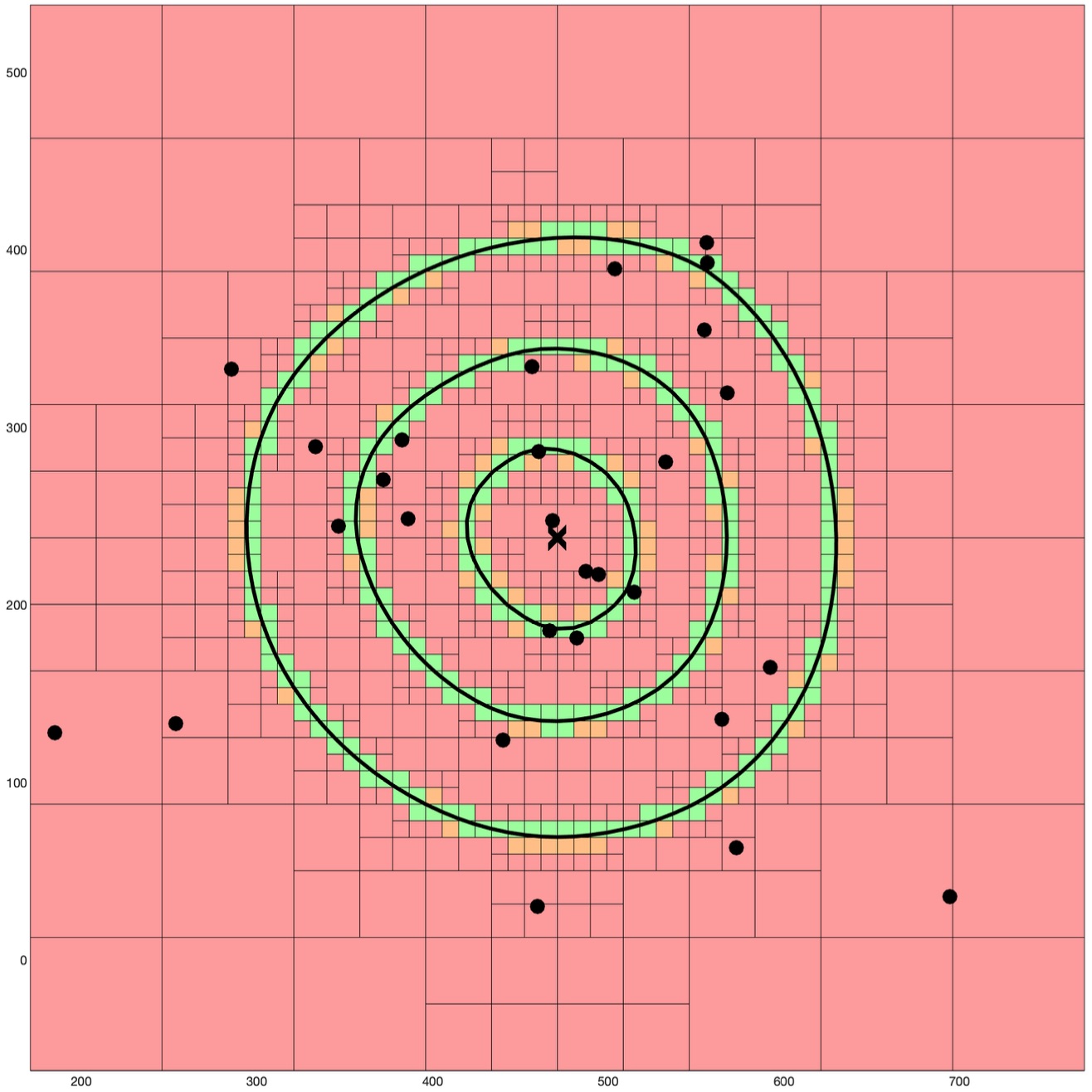
Box subdivision for computing the 28-ellipses of 3 radii.

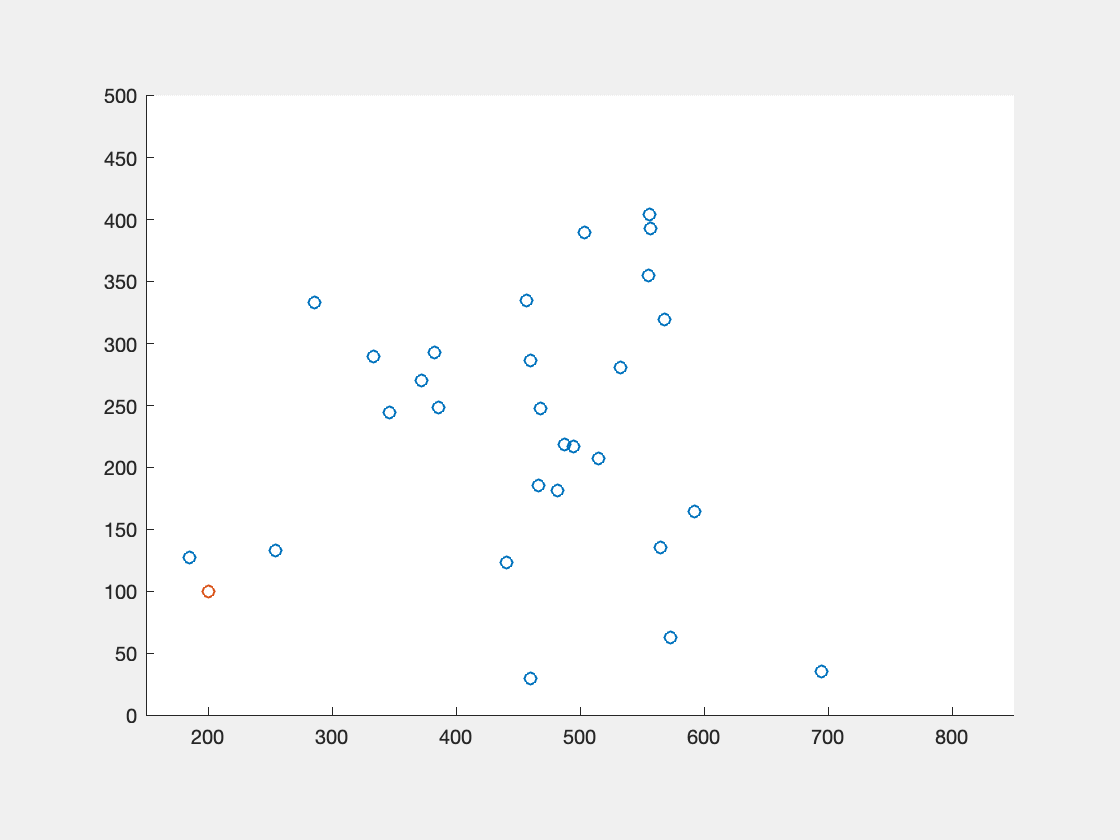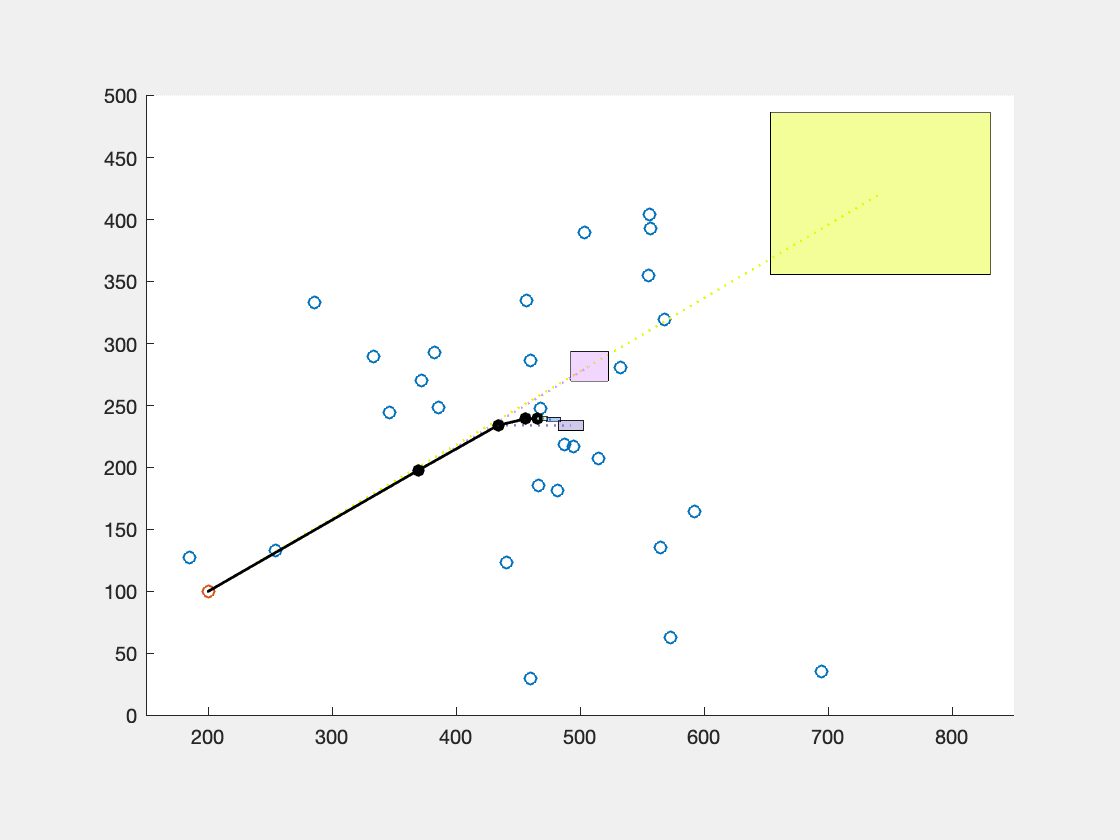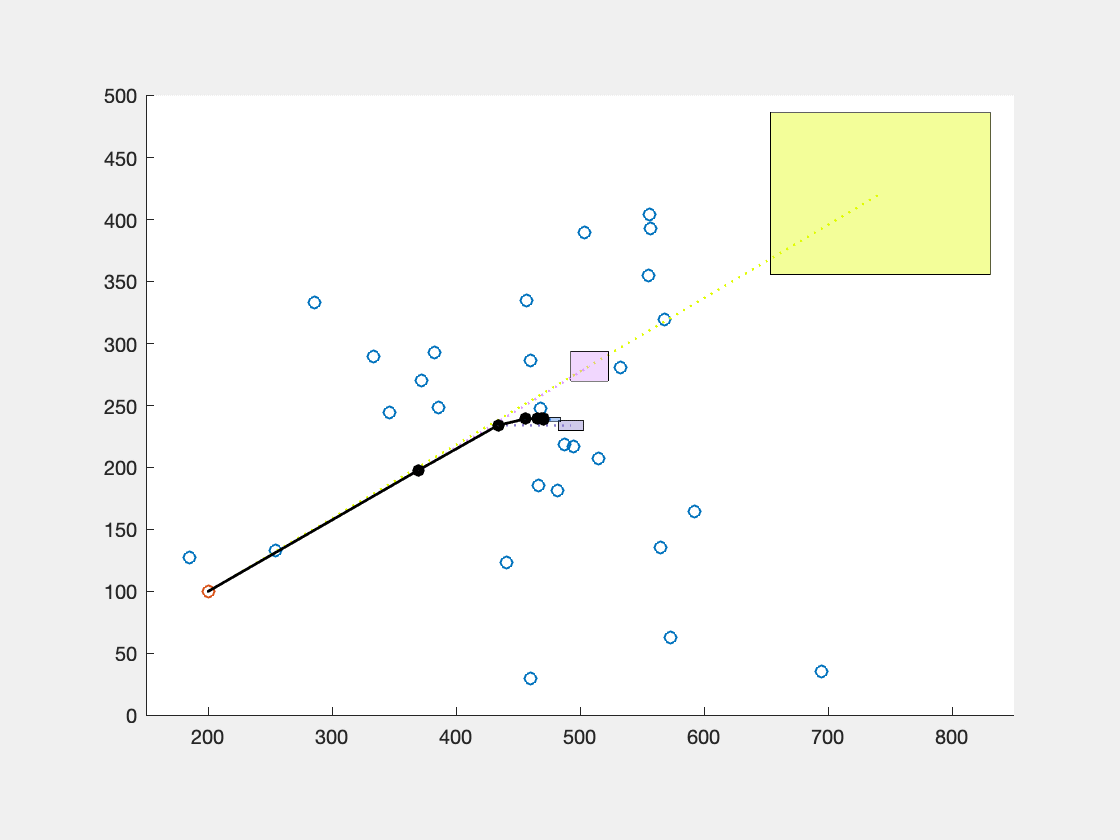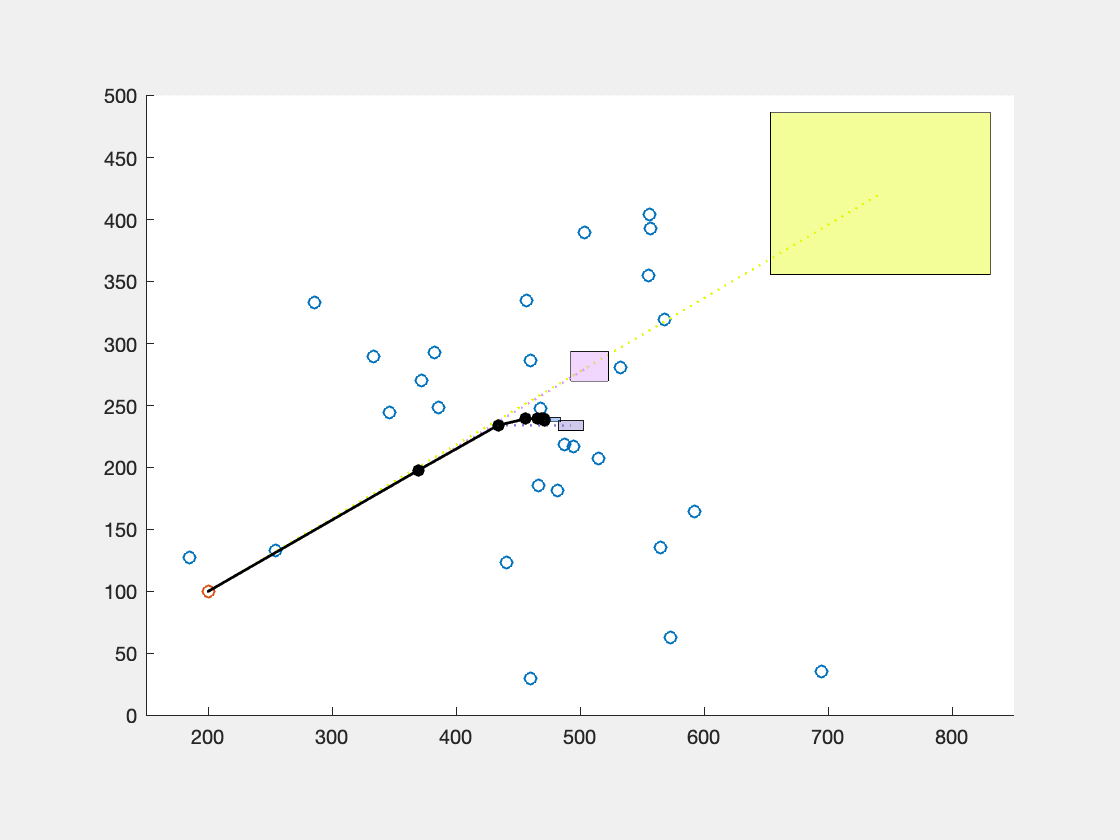
Another approach on finding an approximation of the Fermat point is using a well-known pointsequence constructed by Weiszfeld/Ostresh, which converges to the Fermat point. We add a test, based on interval Newton methods, to decide whether the current point is already approximating the Fermat point good enough.
We have implemented our box subdivision and point sequence algorithms in two dimensions for approximating the Fermat point and k-ellipses using Matlab. We have further implemented the two approximation algorithms for the Fermat point in C++. This code can be found here.

Visualization of the pointsequence, which converges to the Fermat point, and also the boxes involved in the tests.

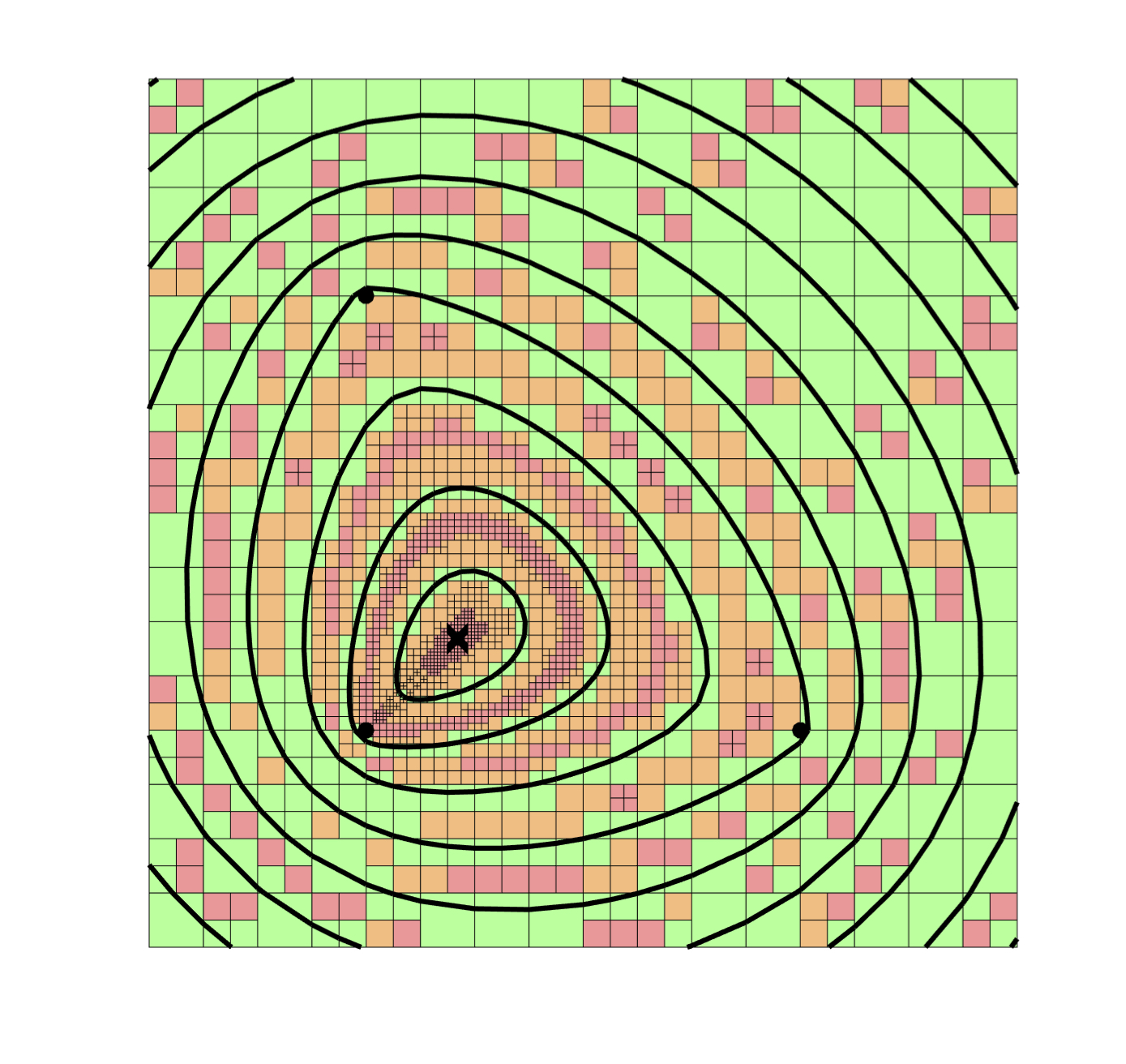A contour plot of 3 foci and with 10 different radii.